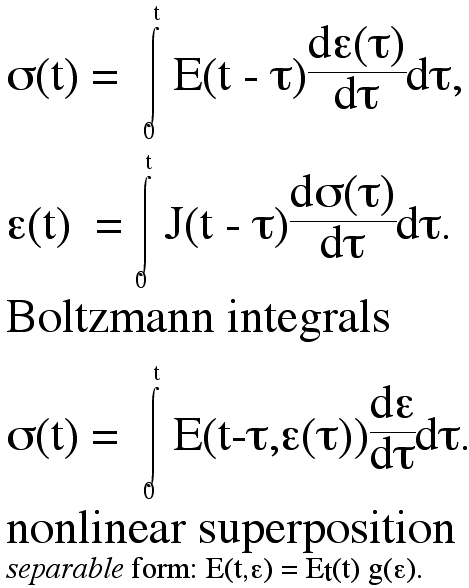QLV quasilinear viscoelasticity
QLV quasilinear viscoelasticity
QLV or quasilinear viscoelasticity refers to a model introduced long ago by Y. C. Fung [1] as a simple way to incorporate both nonlinearity (dependence of properties on load or strain) and time dependence (viscoelasticity) in a simplified integral model.
The QLV model has been used in biomechanics to describe biological tissues. It assumes that the creep compliance J depends on time t and stress σ in a specific way: J(t, σ) = J1(t) f(σ). Similarly the relaxation modulus as it depends on time and strain is assumed to be separable. E(t, ε) = E1(t) f(ε). Many people who use QLV also assume a particular form of time dependent function.
Discrimination among linear and nonlinear models is done by experiment. For nonlinear materials the modulus depends on strain and the compliance depends on stress. For QLV, the shape of the relaxation curves is predicted to be the same, independent of strain. Observation of recovery allows further comparison between models. QLV predicts recovery to follow the same time dependence as creep or relaxation but other theories such as nonlinear superposition allow a different time dependence.
Experiments designed to discriminate among models show that QLV does not properly describe tissue. In soft tissue including tendon, ligament, cornea and others, relaxation rate depends on strain level and creep rate depends on stress level. An experiment done at only one stress level (for creep) or one strain level (for relaxation) is insufficient to discriminate among models. In particular, such an experiment can demonstrate viscoelasticity if time dependence is observed, but it cannot validate QLV. If a stress-strain curve to failure is provided, that can demonstrate nonlinearity but is insufficient to determine what kind of nonlinearity. Similarly, experiments at several strains over a narrow window do not suffice because over a narrow range of strain, variation in biological specimens will obscure the variation in modulus or in compliance.
Experiments to distinguish QLV from other nonlinear models are easy to perform. Do a series of creep tests at different stress level or a set of relaxation tests at different strain levels. Allow sufficient time for recovery between tests.
Constitutive equations are as follows. If the strain is prescribed as a step in time, the stress follows the modulus kernel function within the integral. A subsequent step down in strain gives rise to recovery. Nonlinear superposition is not only superior to QLV in correctly modeling strain dependence of modulus but is actually simpler than QLV because no particular time dependence need be assumed. Also, nonlinear superposition can correctly account for recovery occurring at a different rate than creep, as is observed in the laboratory.

The following Boltzmann integrals represent linear viscoelasticity. For linearly viscoelastic materials, the modulus E(t) determined in a relaxation test depends on time t but is independent of strain; the compliance J(t) determined in a creep test depends on time but is independent of stress. In the equations, t refers to time and τ is a time variable of integration.
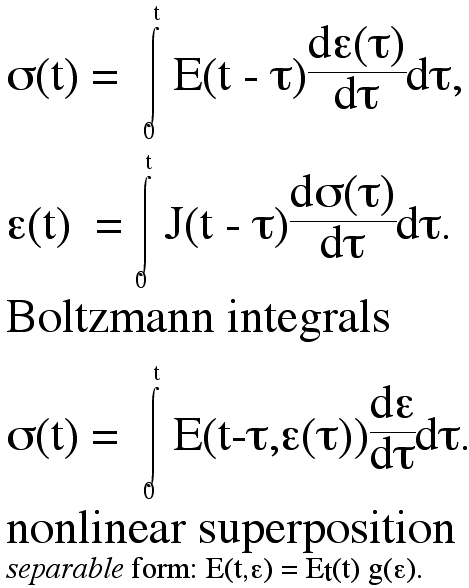
It is by now well known and well established in published experimental studies that QLV does not work for tendon, ligament or other biological tissue. The slope of creep curves depends on stress level and the slope of relaxation curves depends on strain level in contrast to QLV..
Experiment articles and abstracts
Reference
[1] Fung, Y. C., Stress strain history relations of soft tissues in simple elongation, in Biomechanics, its Foundations and Objectives, ed. Fung, Y. C., Perrone, N. and Anliker, M., Prentice Hall, Englewood Cliffs, NJ, 1972.