For general anisotropy there are 903 micromorphic or microstructure elastic constants compared with 21 in classical elasticity.
The constitutive equations for an isotropic micromorphic solid (elastic solid with microstructure) are as follows, following Mindlin.
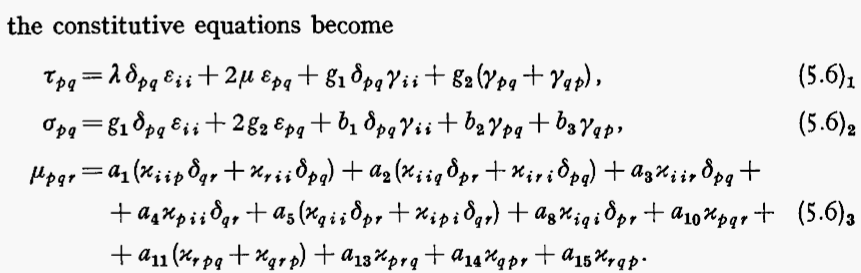
Thte a, b, and g coefficients are elastic constants. Lambda and mu are elastic constants.
Cosserat elasticity is a special case as follows. The points in Cosserat elasticity rotate but they do not deform. Cosserat elasticity allows a couple stress (moment per area) and allows the stress to be asymmetric.

The micromorphic theory predicts frequency dependence of both shear and longitudinal waves as well as cut-off frequencies at which the group velocity of waves goes to zero.
Void elasticity, after Cowin, corresponds to a special case of micromorphic theory in which there is a local dilatation of points in addition to their rotation, but the points do not rotate. Size effects are predicted in bending but not in torsion.
Microstretch elasticity incorporates the freedom of Cosserat elasticity and of void elasticity. It is a subset of micromorphic theory in that the points translate, rotate and undergo dilatation but they do not deform in arbitrary ways.
Relaxed micromorphic elasticity is another subset of micromorphic elasticity. It is somewhat more general than Cosserat elasticity. It has been studied as an alternate approach to generalized continuum theory by Professors Neff, Huetter, and Rizzi; see P. Neff site.
Experiments exploring micromorphic subsets including Cosserat, void and relaxed micromorphic elasticity are presented in our Cosserat page.
See also R. S. Lakes, "Experimental evaluation of micromorphic elastic constants in foams and lattices", Zeitschrift fur angewandte Mathematik und Physik (ZAMP), 74, Article number: 31 (2023). Micromorphic (microstructure) elastic constants are considered within the context of experimental results for foams and rib lattices, and of subsets such as Cosserat elasticity, void elasticity and reduced micromorphic elasticity. Experimentally, longitudinal wave dispersion and cut off frequencies reveal several of the the micromorphic b coefficients. In static experiments, no size effects are evident in compression for the materials studied. The corresponding micromorphic a coefficients are not distinguishable from zero. By contrast, Cosserat effects are pronounced in these materials.
doi link
References
W. Nowacki, Theory of asymmetric elasticity, Pergamon Press, Oxford, UK, (1985)
R. D. Mindlin, Micro - structure in linear elasticity, Archive for Rational Mechanics and Analysis, 16 51-78 (1964).
A. C. Eringen, Theory of micromorphic materials with memory, International Journal of Engineering Science, 10 (7), 623-641 (1972).
A. C. Eringen, Microcontinuum field theories, Springer, New York, NY, (1999).