 Materials with viscoelastic stiffness greater than diamond
Materials with viscoelastic stiffness greater than diamond
Materials with viscoelastic stiffness greater than diamond, adapted from
T. Jaglinski, D. Kochmann, D. S. Stone, R. S. Lakes, Science 315, 620-622, Feb. 2 (2007)
Abstract
We show that composite materials can exhibit a viscoelastic (Young's) modulus far higher than that of either constituent. The modulus (but not strength) was observed to be substantially greater than that of diamond. These composites contain barium titanate inclusions, which undergo a volume change phase transformation if not constrained. In the composite the inclusions are partially constrained by the surrounding metal matrix. The constraint stabilizes the negative bulk modulus (inverse compressibility) of inclusions. This negative modulus arises from stored elastic energy in inclusions, in contrast to periodic composite metamaterials which exhibit negative refraction via inertial resonant effects. Conventional composites with positive stiffness constituents have aggregate properties bounded by a weighted average of constituent properties; their modulus cannot exceed that of the stiffest constituent.
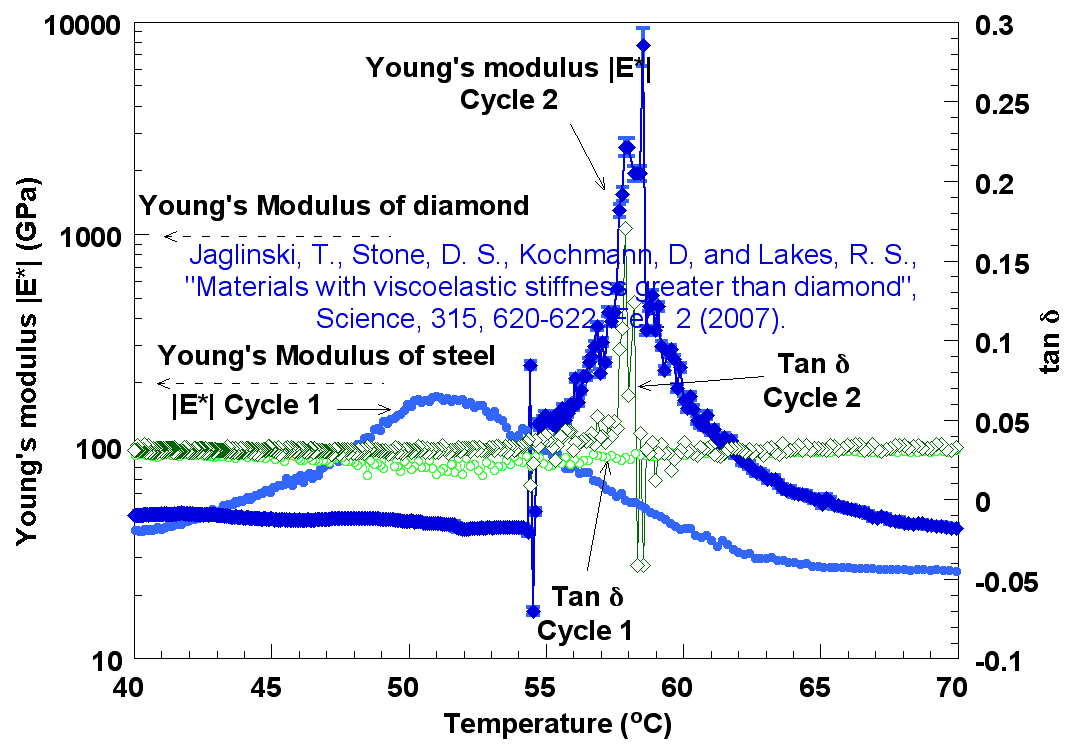
These materials are stiffer than diamond over a range of temperature as determined by dynamic mechanical spectroscopy.
View article in web form from Science or get pdf from here.
Blurb from Nature.
Download supporting online material pdf from Science or from here.
Frequently asked questions and answers.
Here is a related paper which provides analysis of stability.
W. Drugan, "Elastic composite materials having a negative stiffness can be stable" Physical Review Letters 98, 055502, (2007) get pdf
Text of the article
In most elastic systems, a deformed object experiences a force with a component in the same direction as the deformation, so stiffness is positive. Negative structural stiffness (force / displacement ratio) can occur in pre-strained objects such as tubes buckled to form kinks, which contain stored energy at equilibrium (1). Experimentally, negative structural stiffness has been observed in lumped buckled systems composed of rubber tubes (2) and models of single foam cells (3).
The elastic modulus, a stress-strain ratio, is a measure of material stiffness. Negative modulus is anticipated in the context of Landau's (4) theory of phase transformation. As temperature T is lowered from a value above the transformation temperature, an energy function of strain and temperature (Fig. 1, see original article) with a single minimum gradually flattens, then develops two minima or potential wells. If the strain is a shear strain, the transformation is martensitic; for a hydrostatic strain, it is a volume change transformation. The curvature of this energy function represents an elastic modulus, so flattening of the curve corresponds to a softening of the modulus near a critical temperature Tc, a phenomenon observed experimentally. Below Tc, the reversed curvature at small strain represents a negative modulus. Negative modulus, in which the force which deforms an object is in the opposite direction as the displacement, is distinct from negative Poisson's ratio in which a material expands laterally when stretched (5-7). A negative modulus may occur in a pre-deformed object; it is then a negative incremental modulus. An object with all free surfaces and a negative modulus is unstable. A negative shear modulus causes bands or domains to form, even if the surfaces are constrained. A solid object with negative bulk modulus (inverse compressibility) can be stabilized by constraint of the surfaces (8) in contrast to fluids (9). Negative incremental compressibility has been observed in small-cell foams (10). Negative compressibility differs from negative thermal expansion (11) which means stable contraction of an unconstrained object due to temperature increase.
Negative stiffness can give rise to extreme values of physical properties in heterogeneous systems. For example, both negative stiffness and resulting giant damping were observed (2) in a lumped system containing discrete buckled tubes. A composite with negative stiffness inclusions is predicted to give rise to material properties greater than those of either constituent (12,13). Such behavior exceeds classical bounds (14) in which composite properties cannot exceed the properties of the constituents. These bounds are theorems assuming each constituent initially contains no stored energy. Negative stiffness entails initial stored energy; viscoelastic dissipation, if present, enhances composite stability. In composites (15), anomalous high viscoelastic damping was observed and attributed to negative shear modulus in ferroelastic inclusions partially constrained by the matrix. These inclusions were sufficiently small that some of them were single domains. Similar composites (16) of higher concentration exhibited instability as predicted by composite theory incorporating negative shear modulus.
Composite materials were prepared with inclusions of barium titanate (BaTiO3) in a tin matrix. Barium titanate was used since it is a ferroelastic (also a ferroelectric) solid which exhibits a crystal volume change and a crystal shape change during phase transformations, specifically cubic to tetragonal at Tc near 120 degrees C and tetragonal to orthorhombic near 5 degrees degrees C. The rationale for considering this class of phase transformation is that we can have negative bulk modulus K in a constrained inclusion and yet still have stability. Constraint by the matrix restrains the transformation over a range of temperature. Inclusions were by design sufficiently large to contain many domains below Tc. The bulk modulus of a material affects its stiffness in bending but not in torsion since bending entails local volume change.
Polycrystalline barium titanate was fragmented and sieved to achieve a particle size distribution between 210 and 150 mm. Domains in such materials can be smaller than 1 mm. Some particles were plated with nickel to improve interface quality. Composites were fabricated using plated or unplated particles of the same pre-plated sizes. Dispersion of particle inclusions was achieved through an ultrasonic casting technique (17). Specimens (18) were sectioned from ingots using a low speed diamond saw into rectangular cross sections, typically 2 mm x 2 mm x 3.5 cm, or were cut into cylinders, with diameters of 2.6 mm and 3 cm long, using a wire electric discharge milling machine. Digital optical micrographs of polished composite specimens were taken. Specimens were tested in bending using broadband viscoelastic spectroscopy (19). This instrument, which is capable of isothermal internal friction studies over eleven orders of magnitude in frequency, was modified to allow operation up to 300 degrees C and to detect spontaneous strain exceeding 10-4. The viscoelastic response was measured at 100 Hz in bending, well below any natural frequency. Torque was applied electromagnetically and deformation was measured via a laser method. Temperature was monitored with a thermocouple in the air flow within 1 mm of the specimen, to avoid interference with viscoelastic measurement. Heating and cooling rates were 0.05 to 0.5 degrees C / s. The procedure is typical of viscoelastic studies upon materials including those which undergo transformation.
Of thirteen specimens with plated inclusions, all exhibited anomalous viscoelastic response in bending. Anomalous response is defined as a change in modulus or damping larger than could be accounted for via composite theory (20) assuming positive inclusion modulus of any value between zero and infinity. Three exhibited large anomalies and three exhibited a Young's modulus (|E*|, absolute value of the complex viscoelastic modulus) greater than that of diamond. Since all materials exhibit some damping, any measured modulus is a viscoelastic modulus. Of fifteen specimens with unplated inclusions, eleven exhibited anomalous response, and one exhibited a Young's modulus greater than that of diamond. It is theorized that the degree of anomalous response depends on the quality of the inclusion-matrix interface. No anomalous behavior was observed in torsion. The microstructure of a specimen from the latter series, with 10% by volume inclusions, is shown in Fig. 2 (see original article). Modulus and damping (tan delta with delta the phase between stress and strain) of this specimen are shown in Fig. 3. Given the modest damping, the magnitude of the modulus |E*| exceeds the real part E' by only about 2%. Young's modulus exceeds that of diamond over a narrow range of temperature: the composite is stiffer than diamond. Transient negative viscoelastic damping tan delta indicates release of stored energy from the inclusions. Although they are stiff, these materials are not expected to be unusually strong or hard. Negative specific heat was observed in those specimens which exhibited the largest mechanical effects (18). This behavior is consistent with negative bulk moduli of the inclusions since the theoretical specific heat depends on constituent bulk moduli (21).
Behavior of all composites changed with thermal cycling, as was also observed in composites (16) with VO2 inclusions; peaks tended to shift to higher temperatures and to attenuate with cycling. Composites with plated inclusions maintained their behavior over a greater number of cycles than did materials in which inclusions were not plated. The interface is therefore clearly important in determining the behavior. Extreme elastic anomalies were observed for as many as five cycles in a particular specimen. Composite analysis (13) shows that macroscopic strain can be magnified locally by several orders of magnitude in the vicinity of the inclusions during the phase transformation. The macroscopic strain amplitude (less than 4 x 10-6 in these experiments) can therefore give rise to local strain sufficient to cause yield in the tin matrix. This amplified local strain can account for the cycle dependence which could be ameliorated by using a stronger matrix.
Broad peaks in damping tan delta were also observed, as shown in Fig. 4. We remark that even modest effects in these composites are significant since for a dilute particulate morphology, composite properties are known (14,20) to be relatively insensitive to inclusion properties when they have positive modulus. For example, with a 10% concentration of particles, the composite modulus |E*| due to infinitely stiff inclusions is predicted to increase by 22% compared with pure matrix. The composite damping due to inclusions with a peak damping tan delta = 0.06, corresponding to bulk barium titanate, is predicted to be only 6% greater than that of the matrix. The damping peaks shown in Fig. 4 (8% inclusion concentration) correspond to a factor of two increase compared with "pure" tin (see original article), so, as with the above giant anomalies in modulus, negative compressibility of the inclusions is inferred.
The present extreme stiffness results are based on negative compressibility (inverse bulk modulus K, resistance to volume change) of inclusions, in contrast to the negative shear modulus G (resistance to shape change) in prior Sn-VO2 composites (15) which exhibited large damping but modest (5%) anomalies in modulus. These three dimensional aspects of deformation govern the stability and properties of materials. Positive G and K give rise to a positive definite strain energy, hence stability of an object with free surfaces and no constraint. This corresponds to the usual 'allowable' range of Poisson's ratio n, between -1 and 0.5, allowing negative Poisson's ratio in isotropic solids (5). For the less restrictive condition of strong ellipticity, which entails real, positive velocities of shear and longitudinal waves, G greater than 0 and -4G/3 less than K less than infinity. A strongly elliptic solid constrained at the surface is incrementally stable (22) and has a unique elasticity solution (23), so a range of negative bulk modulus is allowed. A material with negative shear modulus G is unstable with respect to domain formation. Surface energy limits how small a domain can be, so a sufficiently small crystal can be single domain and can operate as a negative stiffness inclusion as was the case in Sn-VO2 composites. There is no such inclusion size limitation associated with negative bulk modulus. An inclusion in a composite is under partial constraint. The corresponding stability condition (24) upon the moduli is intermediate between positive definiteness and strong ellipticity, allowing a stable negative bulk modulus under quasistatic conditions.
Diamond has long been considered to have maximal properties such as stiffness and hardness. Achievement of substantially greater stiffness illustrates the significance of composites with negative stiffness inclusions. These composites are stiffer than diamond over a temperature range. They offer potential in high performance materials in which high stiffness or high dissipation are of use. They may occur naturally in rocks and play a role in deep focus earthquakes.
References and notes
1. J. M. T. Thompson, Philos. Trans. R. Soc. Lond. 292, 1 (1979).
2. R. S. Lakes, Philos. Mag. Lett. 81, 95 (2001).
3. P. Rosakis, A. Ruina, R. S. Lakes, J. Materials Science 28, 4667 (1993).
4. L. D. Landau, in Collected papers of L. D. Landau, ed. D. Ter Taar, Gordon and Breach / Pergamon, NY, London (1965).
5. R. S. Lakes, Science, 235, 1038 (1987).
6. A. Y. Haeri, D. J. Weidner, and J. B. Parise, Science, 257, 650 (1992).
7. R. H. Baughman, J. M. Shacklette, A. A. Zakhidov, S. Stafstrom, Nature 392, 362, (1998).
8. Within continuum mechanics, there is no size limitation for a constrained object of negative bulk modulus to be stable. Thermodynamics suggests a size dependent metastability associated with negative compressibility, owing to the nonzero size of atoms and nonzero temperature. The time scale for such metastability in solids may, however, exceed experimental time scales. Indeed, diamond itself is metastable.
9. J. Van der Waals, thesis, University of Leiden, (1873), English translation J. R. Rowlinson, Ed. North Holland, Amsterdam, p. 254, (1988).
10. B. Moore, T. Jaglinski, , D. S. Stone, and R. S. Lakes, Philos. Mag. Lett, 86, 651, (2006).
11. T. A. Mary, J. S. O. Evans, T. Vogt, A. W. Sleight, Science 272, 90, (1996).
12. R. S. Lakes, Phys. Rev. Lett., 86, 2897, (2001).
13. R. S. Lakes, W. J. Drugan, J. Mech Phys. Solids 50, 979 (2002).
14. Z. Hashin and S. Shtrikman, J. Mech. Phys. Solids, 11, 127 (1963)
15. R. S. Lakes, T. Lee, A. Bersie, Y. C. Wang, Nature 410, 565 (2001).
16. T. Jaglinski, R. S. Lakes, Phil. Mag. Letters 84, 803 (2004).
17. Y. Yang, J. Lan, X. Li, Mater. Sci. Eng. A 380, 378 (2004).
18. Information on materials, methods, and interpretation can be found on Science online.
19. T. Lee, R. S. Lakes, A. Lal, Rev. Sci. Instrum. 71, 2855 (2000).
20. Z. Hashin, J. Applied Mechanics, 29, 143 (1962).
21. B. W. Rosen and Z. Hashin, Int. J. Engng. Sci. 8, 157 (1970).
22. Kelvin, Lord (Thomson, W.), Philos. Mag. 26, 414 (1888).
23. E. Cosserat and F. Cosserat, C. R. Acad. Sci. Paris 126, 1089 (1898)
24. W. J. Drugan, "Elastic composite materials having a negative stiffness can be stable" Physical Review Letters 98, 055502, (2007)
25. Partial support by the National Science Foundation and by the NSF MRSEC Program is gratefully acknowledged. We thank W. Drugan for stimulating discussions.
More recently, even higher stiffness has been attained using a similar paradigm of phase transforming inclusions in a matrix. Stable singular structural stiffness has been attained using a different paradigm involving nonzero energy flux; for reprints see negative stiffness link at top. Stable negative stiffness is also demonstrated. We have not called these metamaterials or architectured materials or architected materials or active materials; these designations have become popular.
More extremal materials
Top
